Módulos y redes.
Guión.
Introducción.
1. Módulos y redes. concepto.
1.2. Concepto de estructura.
1.3. El canon.
1. Canon de perfil de los antiguos egipcios.
2. El canon de los escultores griegos del siglo V a. C.
1.4. Concepto de red.
1. Redes planas.
2. Redes espaciales.
1.5. La malla.
1. Redes y mallas.
1.6. Módulos, mosaicos y redes en la naturaleza.
Estructuras modulares naturales
Mundo orgánico e inorgánico
1. Módulos en el mundo orgánico
2. Módulos en el mundo
inorgánico.
1.7. Estrategias de composición modular.
1. La tensión.
2. Los submódulos y súper
módulos.
3. Diferente
forma, color, textura.
4. Combinaciones
5. Distorsiones.
6. Ambigüedad
figura – fondo.
7. Mezcla de
redes.
1.8. Aplicaciones de la teoría modular en
las artes visuales.
2.
Relaciones entre la estructura y la proporción en la creación de formas
bidimensionales y tridimensionales.
2.1. La
razón
2.2. La proporción.
A. La igualdad.
B. Semejanza, homotecia y
escala.
C. La
proporción áurea.
2.3. Rectángulos
irracionales.
2.4. Proporción cordobesa, el
rectángulo 4/3.
2.5. Le Modulor de Le Corbusier.
2.6. Las
simetrías.
1. Traslación.
2. Reflexión.
3. Giro.
4. Desplazamiento.
5. Identidad.
2.7.
Interacciones formales.
1.
Distanciamiento.
2. Toque.
Contacto.
3. Superposición.
4. Penetración.
5. Unión.
6. Sustracción.
7. Intersección.
8. Coincidencia.
2.8. Estructuras modulares bidimensionales.
1. Coordinación modular
bidimensional
Módulos simples planos.
A. El cuadrado:
B. El triángulo equilátero:
C. El hexágono:
D. El rombo:
E. La circunferencia:
F. El supermódulo.
2. Coordinación modular
bidimensional
Módulos compuestos planos.
2.9. Estructuras modulares tridimensionales.
Coordinación modular
tridimensional
A. La forma.
B.
La imagen.
C. La figura.
D. Estructuras.
1. Módulos simples
tridimensionales.
A. El cubo
B. El prisma.
C. Cuboctaedro.
D. Octaedro truncado, tetracaidecaedro, o poliedro de Lord Kelvin.
E. Rombododecaedro, o
dodecaedro rómbico.
2. Módulos
compuestos tridimensionales.
A. Cuboctaedro
y octaedro
B.
Cubo truncado u octaedro.
2.10. El Mosaico.
1. Mosaicos formados por una sola tesela y que sea un polígono regular.
A. El cuadrado.
B. El triángulo equilátero.
C. El hexágono regular.
2. Mosaicos formados por dos
tesela y que sean polígonos regulares.
E. Triángulo y
hexágono.
F. Octógono y
cuadrado.
G. Dodecágono y
triángulo
H. Hexágono,
cuadrado y triángulo.
I. Hexágono,
cuadrado y dodecágono
J. Cuadrado y
triángulo
K. Hexágono y
triángulo
L. Cuadrado y
triángulo
3. Polígonos no regulares que rellenan el plano.
4. Mosaicos por deformaciones de los polígonos.
3. Estructuras
modulares artificiales. Aplicaciones en el arte.
Ejemplos de
estructures modulares artificiales.
Resumen
Preguntas
de autoevaluación.
Bibliografía.
Bibliografía
comentada.
Introducción.
El dibujo técnico es un lenguaje
visual universal que permite expresar ideas objetivamente. Parte del dibujo
técnico está sustentado en la geometría que es una rama de la matemática. Un
concepto al mismo tiempo de matemática y de dibujo es el módulo. Una figura que
se repite es una módulo. Desde la antigüedad los creadores visuales han tomado
el concepto de módulo para realizar
composiciones, repitiendo una misma figura hasta el infinito. Estas obras se
las ha llamado composiciones modulares. Las redes son las líneas geométricas
sobre las que se ordenan los módulos. La creatividad del ser humano intuyó que
a los módulos se les puede transformar mediante giros, traslaciones, aumentos,
disminuciones y varias simetrías, lo que permitió una mayor riqueza y
expresividad de las composiciones modulares. Las aplicaciones prácticas son
abundantes, pavimentos, alicatados, cenefas, tapices, tejidos, bordados,…
Durante el siglo XX los artistas cogieron las ideas del módulo de la artesanía
para trasladarlo a composiciones de mayor envergadura, y el diseño gráfico
moderno también se ha servido en el.
Este tema hará un recorrido desde
el módulo, la red, las estructuras modulares y sus relaciones de
proporcionalidad, entendida en las creaciones bidimensionales y
tridimensionales.
1. Módulos y redes. concepto.
El módulo en matemática es un
número que se usa en comparación con otros y se toma arbitrariamente como
unidad. Por extensión en artes visuales, se entiende que es una dimensión que
se toma como unidad de medida, norma, modelo o patrón La acepción más conocida
del módulo es como parte de un todo que se utiliza como unidad en una
construcción, para establecer las dimensiones y proporciones de un conjunto.
Por ejemplo: la arquitectura utiliza un módulo como medida, para realizar todas
las dimensiones del edificio. En la arquitectura clásica, el módulo era la
medida del radio del fuste de la columna en su parte inferior. Son módulos
célebres:
El Módulo vitruviano; el módulo
de Policleto, que toma la cabeza humana; el módulo de Le Corbusier, que utiliza
el cuerpo humano en sección áurea; el módulo Hele de Rafael Leoz, un módulo con
forma de ele, formada por cuatro cubos.
Otra acepción en artes visuales
es que el módulo es la forma elemental que se repite múltiples veces y llega a
llenar el espacio bidimensional o tridimensional. Por ejemplo: el diseño modular
utiliza una parte que se repite, es autónoma y se puede intercambiar para
realizar un diseño.
La aplicación práctica del módulo
más conocido son los mosaicos. Los polígonos regulares pueden formar un mosaico
periódico si repetimos una forma poligonal como módulo. Sólo hay tres polígonos
que con la misma loseta puedan cerrar un espacio plano sin dejar huecos son: el
triángulo equilátero, el cuadrado, y el hexágono regular.
En la historia del arte han sido
muchas las aplicaciones del módulo para realiza composiciones, como:
Las Teselas en los mosaicos
romanos, hechos de pequeñas piezas en forma de cubo, de mármol, vidrio o pasta,
para realizar los pavimentos. Los azulejos de la Alhambra de Granada, ladrillos vidriados, pequeños de
colores para revestir paredes de cocinas y baños. Baldosas, cerámicas y losas
en los recubrimientos de Antonio Gaudí que
utiliza el hexágono regular en el suelo del Paseo de Gracia de
Barcelona.
La Alhambra de Granada posee
mosaicos derivados de la descomposición del cuadrado. El hueso nazarí, es la
deformación de un cuadrado base. El avión o pájaro volador es un giro de 90 º
del rectángulo original. La pajarita nazarí, es la deformación del triángulo
equilátero, y luego sujeto asimetrías y giros.
Mosaico de la Alhambra de Granada. Arte nazarí.
Mosaicos de San Vital de Rávena.
Módulos
Figura elemental geométrica u orgánica que se repite
Triángulo equilátero. Módulo y red de triángulos equiláteros, que forma hexágonos regulares
Red
La red consta de filas
y columnas de módulos
y recubre
el plano o el espacio
Super módulo.
Red de cuadrados con el dibujo de una hoja que forma un super modulo para componer el mosaico de la hoja de la Alhambra de Granada.
1.2. Concepto de estructura.
Un módulo es la unidad más pequeña que
organiza una estructura, también es el elemento que estructura la forma.
Un sinónimo en matemáticas sería el múltiplo. La suma de la unidad modular da lugar a otras mayores. Un conjunto de módulos dan lugar
a la estructura que es la relación que mantienen entre sí las partes de un
todo. Las partes son individuales pero al mismo tiempo interdependientes. En
artes visuales es el modo de organizar las partes de un conjunto. Los módulos
repetidos se combinan dando lugar a una estructura de tipo geométrico, y en el
todo pueden aparecer conceptos como proporción, ritmo y movimiento.
Ejemplos sería la estructura
atómica de los elementos, o la estructura ósea, o en construcción
arquitectónica o ingeniería la estructura es el armazón que soporta una obra.
Por ejemplo, la estructura de un puente reticulado, como el viaducto de
Trenton, sobre el río Delaware, 1804-06 con cerchas Pratt, de Theodore Burr.
Estructura
Estructura (Esqueleto), características invariables..
Formas organizadas con otras formas, creadas (naturales) o construidas (artificiales). Repetición de un modulo 2D o 3D.
1.3. El canon.
La escultura de la misma forma
que la arquitectura ha tomado el concepto de módulo como una parte de la
totalidad que se utiliza para proporcionarla. Así, escultores de la antigüedad,
para proporcionar el cuerpo humano utilizaron como unidad de medida alguna
parte del cuerpo. Este es el nuevo concepto conocido como “canon”, que es regla, medida, modelo, y es equiparable al módulo en arquitectura que
regula todas las partes de la obra. El concepto de canon se utiliza para
expresar el conjunto de normas que hay en la proporción y la simetría en artes
visuales tridimensionales, y en concreto se refiere a las obras del mundo
clásico griego y romano. En arquitectura el canon está relacionado con los
antiguos órdenes arquitectónicos griegos.
1. Canon de perfil de los antiguos egipcios.
El canon de los antiguos egipcios
se refiere a la representación de la cabeza, brazos y piernas de perfil,
mientras que hombros y tronco se representaban de frente. El módulo era tomado
con la anchura de la mano, el brazo y el puño cerrado, y el codo. El cuerpo
humano se representaba con un módulo de 18 a 21 puños dependiendo de la época.
2. El canon de los escultores griegos del siglo V a. C.
Los escultores griegos del siglo
V a. C. utilizaron cánones de proporción, por ejemplo el canon de Policleto.
La medida del canon de Policleto
era la cabeza y estaba contenida unas siete veces y media dentro del cuerpo.
Policleto de Argos, obra del Diadúmeno. Canon de !/7 cabezas
Policleto de Argos, obra El Doríforo. Canon de !/7 cabezas
Posteriormente este módulo se
amplio a ocho cabezas con Lisipo en la estatua Apoxiomeno; y ocho y media con
el artista Leócares en su obra el Apolo del Belvedere.
Los cánones se retoman por
Leonardo da Vinci, Alberto Durero y León Battista Alberti en el Renacimiento
italiano.
Lisipo, escultura del Apoxiomeno. Canon de 1/8 cabezas
Leócares, obra del Apolo del Belvedere. Canon de 1/ 8,5 cabezas
Miguel Ángel. Obra David, 1501 - 1504
siguiendo los cánones de la escultura grecolatina
Alberto Durero. Pintura de Eva 1507. Canon de 1/9 cabezas
1.4. Concepto de red.
La red
es un conjunto estructurado de módulos y conectados entre sí, con un patrón
característico.
La red
permite superponer, organizar, circular, o componer elementos o formas. Es la
manera más sencilla de dividir el espacio con una regularidad, por ejemplo con
estructuras de polígonos, como un papel milimetrado o isométrico.
La red en
un plano consta de filas y columnas de
módulos que lo recubre. La intersección de los módulos de la red se llama
nodos. El espacio también se puede
organizar en módulos como las celdas en cristalografía. El apilamiento de los
cristales minerales es un ejemplo de redes espaciales.
1. Redes planas.
Dentro del campo del dibujo es un
buen ejemplo de red el papel milimetrado y el papel isométrico que proporcionan
una base para componer dibujos. A modo de analogía podemos ejemplificar las
redes en las porterías de fútbol.
2. Redes espaciales.
La proyección tridimensional de
las redes planas se transforma en redes tridimensionales.
1.5. La malla.
En una tipología en malla cada
nodo tiene una conexión con todos los nodos de la red, además la malla es una
red que no deja espacios huecos en su estructura. La retícula en malla puede
ser bidimensional o tridimensional, permite la localización y ubicación de
puntos y de figuras.
1. Redes y mallas.
Las redes y mallas pueden ser
simples, cuando su estructura consta de un solo polígono y compuestas, cuando
están formadas por dos o más polígonos
1.6. Módulos, mosaicos y redes en la naturaleza.
Estructuras modulares naturales
Mundo orgánico e inorgánico
La naturaleza que es la mejor
constructora utiliza con frecuencia módulos y estructuras modulares orgánicas.
Los vegetales y animales han
evolucionado con módulos básicos que se repiten y crean una estructura.
También se dan casos donde son
los propios seres vivos los que crean el módulo y la estructura, como
construcciones exteriores a su cuerpo. El ejemplo más paradigmático son las
celdas hexagonales de los panales de las abejas. Las abejas solucionaron el
problema de una superficie de máximo volumen con el mínimo de superficie hace
mucho tiempo. Algunos ejemplos macroscópicos y microscópicos de la utilización
del módulo en la naturaleza serían los siguientes:
1. Módulos en el mundo orgánico
Las escamas en los reptiles,
serpientes, lagartos, iguanas,…
Los caparazones de las tortugas.
Las casillas
de las colmenas.
Los ojo
de los insectos, como el ojo de una mosca.
Las alas
de las mariposas.
Los
granos de maíz en la mazorca de maíz.
Los
racimos de las uvas.
El
pelaje sobre algunos mamíferos, por ejemplo la jirafa y su retícula irregular.
El
módulo de los gusanos.
2. Módulos en el mundo inorgánico.
Las redes
espaciales en los cristales minerales.
Las redes
espaciales de una sustancia cristalina se obtiene por repetición de la celda
unidad.
La
estructura atómico de los elementos químicos como el carbono
La
redes de Bravais en mineralogía.
1.7. Estrategias de composición modular.
Cuando se realiza una composición
modular es posible crear mayor interés visual con algunas estrategias como:
1. La tensión.
La tensión se puede agudizar si
el módulo es irregular o curvado.
2. Los submódulos y súper módulos.
La combinación de diversos módulos básicos o
submódulos forman una figura más compleja llamada súper módulo.
3. Diferente
forma, color, textura.
El color, forma y textura diversa pueden dar
un interés visual a la composición.
4. Combinaciones
Los módulos se pueden combinar para añadir
interés y crear ritmo en la composición, algunas de estas composiciones serían:
combinar módulos rectos y curvos, ordenarlos con forma espiral, circular,
sinuosidad, zigzagueante,…Los módulos también se pueden disponer con giros, superposiciones, tocamientos,
alternancias, simetrías…
5. Distorsiones.
El módulo se puede distorsionar mediante las
transformaciones geométricas. Un módulo origen se distorsiona y cambia de forma
en la composición, por homotecia, afinidad, u
homología, el objetivo final es desarrollar la expresividad.
6. Ambigüedad
figura – fondo.
Trabajar la ambigüedad de la figura y fondo
da resultados interesantes para jugar con la percepción.
7. Mezcla de
redes.
La combinación de redes de diferentes tipos
proporciona resultados poco comunes que atraen la atención al espectador.
1.8. Aplicaciones de la teoría modular en las artes
visuales.
El movimiento artístico como el
Op Art, utiliza submódulos para dar impresión de tridimensionalidad sobre la
superficie plana. Artistas que en sus creaciones han utilizados los módulos
son: Víctor Vasarely y Maurits Cornelis Escher, los mosaicos creativos de Escher son célebres. Piet Mondrian crea composiciones con cuadrados y colores puros.
El pintor alemán Paul Klee, compone acuarelas con módulos y puntos de color,
que tienden a la abstracción. En España el escultor Eusebio Sempere con una
obra abstracta de repeticiones geométricas es un buen ejemplo, o Andreu Alfaro
Hernández que aplica sus principios geométricos a obras abstractas por
repetición de un módulo.
2. Relaciones entre la estructura y la proporción
en la creación de formas bidimensionales y tridimensionales.
Los módulos son formas
geométricas con unas magnitudes y tamaños en sus lados. Estas formas al
relacionarse con otras interactúan estableciendo relaciones de proporción. La
proporción es la relación que hay entre las partes y el todo. Al establecer
correspondencias y comparaciones con los módulos la percepción casi de forma
intuitiva nos informa de su armonía. La relación entre las cosas en arte tiene
importancia porque es el medio de crear unidad dentro de la diversidad.
La proporción es un concepto que
se ha utilizado en todas las artes visuales y en todas la historia del arte,
para buscar belleza. Una de las concepciones más influyentes ha sido la belleza
como proporción matemática que lleva a Pitágoras y los pitagóricos a los
números. Los seres existen a imitación de los números. Los principios de las
matemáticas son los principios de los seres reales, y los números son la
naturaleza del Universo. Los pitagóricos asignaron un número a cada cosa y se preguntaron de
donde procedían los números que es como plantear de donde proceden los seres
reales. Los números son eternos e inamovibles y “todas las cosas son números “.
Los comportamientos y propiedades de los seres reales del universo pueden
describirse mediante números. La ciencia se ha aprovechado de este supuesto
pitagórico y lo ha corroborado.
Las derivaciones prácticas de
estas ideas tuvieron su aplicación en manifestaciones artísticas, con respecto
al cuerpo humano y su representación, la
concreción de cánones de proporción basados en números.
Además de utilizar la proporción en los
cánones de proporcionalidad del cuerpo humano, se aplicó a la arquitectura con
el diseño de los edificios según un módulo base. Los tipos arquitectónicos
griegos utilizan el radio del tambor de una columna que sirve de módulo para su
altura.
El módulo es la unidad más pequeña que organiza
una estructura, también es el elemento que estructura la forma. La suma
de la unidad modular da lugar a una
estructura mayor. La estructura es la
relación que mantienen entre sí las partes con el todo. Las partes son
individuales pero al mismo tiempo interdependientes, esta conexión puede venir
determinada por relaciones de proporcionalidad.
Los módulos repetidos se combinan
dando lugar a una estructura de tipo geométrico bidimensional o tridimensional
como se ha estudiado anteriormente. A continuación, se enumerarán estas
conexiones proporcionales. Para comprender las relaciones de proporcionalidad
entre los módulos definiremos algunos términos fundamentales como: la razón, la
proporción y la igualdad; para después estudiar las relaciones de
proporcionalidad como: la semejanza, la homotecia, la escala, la
proporción áurea, los rectángulos
irracionales, la proporción cordobesa, y las simetrías.
2.1.
La razón
La razón es la comparación de dos
cantidades.
La razón entre dos segmentos es
el vínculo que existe entre ellos, como se relacionan
Es la relación entre dos partes,
puede haber una razón aritmética y una razón geométrica:
La razón aritmética o por diferencia:
Es la diferencia de las dos
cantidades, por ejemplo 6 es a 4, o
también 6 – 4.
Visto de modo gráfico quedaría
así: la razón entre el segmento A y el segmento B es de 6-4
B = 4
La razón geométrica o por cociente:
Es el cociente de las dos cantidades, por
ejemplo, 6 / 4
2.2. La proporción.
La proporción es una relación entre razones,
es una combinación o correlación entre dos o más razones, por ejemplo expresado
de modo matemático:
2/1 = 4/2 = 8/4 = 16/8 = 32/16
Dicho de otro modo es una conservación de la
razón.
A. La igualdad.
Una forma es igual a otra cuando su forma y tamaño son iguales. Al
superponerse coinciden los vértices y las aristas. Si establecemos una razón de
proporcionalidad observaemos que su cociente es uno.
Una forma igual a otra se ha utilizado en artes visuales como módulos para
los mosaicos y la decoración. La aplicación a las figuras iguales de
transformaciones geométricas como el giro, la traslación, las simetrías
radiales, puntuales y por desplazamiento son los fundamentos de los mosaicos.
B. Semejanza, homotecia y
escala.
Dos formas del mismo tipo si tienen una
proporción idéntica se llaman semejantes. Las figuras semejantes tienen la
misma forma pero distinto tamaño, los segmentos son proporcionales y los ángulos
son iguales, y su razón de semejanza es igual. A las figuras homotéticas si se
les aplica una rotación o una simetría axial se dice que son semejantes, tienen
la misma forma pero orientadas de forma distinta.
La semejanza en definitiva es una consecuencia
de la homotecia, es decir: el fenómeno proyectivo donde un vértice de radiación
de punto propio, proyecta una forma contenida en un plano original en otro
plano paralelo. La figura transformada es semejante a la original pero de mayor
tamaño. Por extensión, se está realizando una escala, entre la figura original
y la transformada o dibujada, hay una relación proporcional. En dibujo, la
escala se expresa con un cociente, donde el numerador representa el dibujo, y
el denominador la realidad, por ejemplo: Escala: 1/ 2 que indica que el dibujo
es la mitad que el original.
La semejanza es la base de las cuadrículas (módulo cuadrado) para realizar
ampliaciones o reducciones de dibujos, planos, o mapas. Esta construcción
garantiza la proporcionalidad de los segmentos. Un plano es una figura
semejante al terreno o edificio original, proyectado sobre una pauta modular y
a una escala determinada.
C. La proporción áurea.
La belleza como armonía y proporción de las partes, que derivó de
Pitágoras no se olvidó con el transcurso de los siglos. Áurea es un adjetivo
derivado de oro, el material precioso por excelencia. La proporción áurea es
recogida por Euclides, c. 325 - 265
a . C. en su libro Los
Elementos, donde la expresa como la división de un segmento en media y
extrema razón. Leonardo de Pisa, llamado, Fibonacci, 1170 – 1250, escribió Del Liber abaci, 1202, donde aparece su célebre progresión o serie de Fibonacci. Aquí se encuentra la
famosa proporción áurea: 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,... que si
la expresamos en quebrados queda de la siguiente forma: 1/1, 1/2, 2/3, 3/5,
5/8, 8/13, 13/21, 21/34, 34/55, 55/89, 89/144, 144/233,... = K = Ф = 0,618,... ∞.
El número áureo, o número de oro, es la razón de proporción de la Ф = 0,618,… ∞ . Este número se había
utilizado en las composiciones de las obras artísticas y que aparece en la
naturaleza, por aproximación.
Luca Paccioli, 1445 – 1517 escribe el primer
tratado sobre esta célebre progresión, De
la Divina Proporción
El propósito de buscar la belleza en arte continúa, la belleza terrenal y la belleza celestial. Los dibujos que apareen en el libro son creación de Leonardo da Vinci. Paccioli en Dela Divina Proporción
El propósito de buscar la belleza en arte continúa, la belleza terrenal y la belleza celestial. Los dibujos que apareen en el libro son creación de Leonardo da Vinci. Paccioli en De
La proporción áurea es la única
que es al mismo tiempo aritmética y geométrica. Cada término es la suma de los
dos anteriores, y es media proporcional entre el anterior y el siguiente.
El segmento grande es la suma de
los otros dos segmentos pequeños; el
grande es 8, los pequeños son 5, 3. Tenemos tres segmentos: el total que es 8;
el mayor que es 5 y el menor que es 3. El segmento total es al segmento
mayor, como el mayor es al segmento menor. La relación entre o razón entre los segmentos es el número de oro,
que se designa con la letra griega Φ “fi”, 8/5 = Φ y 5/3
= Φ.
A =3
B = 5
C = 8
Lo importante no son los
segmentos sino la relación que existe entre ellos. Esta relación produce un
placer estético al haber un vínculo
oculto común a los tres segmentos. Este encuentro entre iguales pero distintos,
es el secreto de la proporción, la unidad dentro de la diversidad. La
progresión de Fibonacci, ejemplifica que los términos son iguales pero
diversos.
Rectángulo áureo. Número de oro Φ .
Una de las formas más utilizadas
para encontrar la proporción áurea y el número de oro es construirla a partir
del rectángulo áureo. Se inicia a partir de un cuadrado base. Se dibuja su
mitad. La diagonal de uno de los rectángulos mitad, se abate esta diagonal
sobre la prolongación de la base. El punto de intersección del abatimiento
determina el lado mayor del rectángulo, el lado menor es el del cuadrado
origen.
Paso número 1 Paso número 2
Paso número 3
Si comprobamos las razón entre
los dos lados del rectángulos se comprueba que están en proporción áurea.
a / b = a + b / a
8/ 5 = 13 / 8 = 0,16...∞
a / b = a + b / a
8/ 5 = 13 / 8 = 0,16...∞
Φ = 0,161803 39887 49894
84820 45868 34365
63811 77203 09179
80576,... ∞
Φ = 0,61803 39887 49894
84820 45868 34365
63811 77203 09179
80576,... ∞
La conexión con el tema de los módulos es que
el rectángulo áureo se ha utilizado como módulo en las creaciones de las obras
de arte, y sus divisiones armónicas proporcionan rectángulos semejantes
utilizados en la composición de motivos artísticos. He aquí algunas divisiones
armónicas del rectángulo áureo.
2.3. Rectángulos
irracionales.
Si consideramos que un módulo es la unidad
más pequeña que organiza una estructura. El módulo elemental es el cuadrado
donde la razón entre sus lados es 1/1 =
1. La diagonal del cuadrado vale √ 2 Si aplicamos el teorema de Pitágoras: 1 2 + 1 2 = C 2 podemos averiguar el valor de la diagonal del
cuadrado: 1 + 1 = C 2.
Donde la hipotenusa C = √ 2 =
1,4142135,... ∞.
El cuadrado al mismo tiempo es un racional e irracional, o dinámico y estático, porque tiene razón 1 y diagonal irracional √ 2. Si abatimos la diagonal del cuadrado sobre su base podemos ampliar su forma hasta conseguir un rectángulo. Este nuevo rectángulo tiene por lados 1 y √ 2 , por este motivo se llama rectángulo √ 2 . Un rectángulo irracional es aquel que tiene como razón un número irracional. Las aplicaciones de los rectángulos irracionales en la historia del arte han sido: las proporciones de los órdenes clásicos, plantas de templos, arquitectura modulada como las plantas de iglesias y catedrales, los palacios renacentistas modulados como el Pacio Ruccellai de Alberti, los mosaicos,…
El cuadrado al mismo tiempo es un racional e irracional, o dinámico y estático, porque tiene razón 1 y diagonal irracional √ 2. Si abatimos la diagonal del cuadrado sobre su base podemos ampliar su forma hasta conseguir un rectángulo. Este nuevo rectángulo tiene por lados 1 y √ 2 , por este motivo se llama rectángulo √ 2 . Un rectángulo irracional es aquel que tiene como razón un número irracional. Las aplicaciones de los rectángulos irracionales en la historia del arte han sido: las proporciones de los órdenes clásicos, plantas de templos, arquitectura modulada como las plantas de iglesias y catedrales, los palacios renacentistas modulados como el Pacio Ruccellai de Alberti, los mosaicos,…
2.4. Proporción
cordobesa, el rectángulo 4/3.
La proporción cordobesa es propia de un
rectángulo donde la razón de sus lados es 1,3. El rectángulo tiene la
razón de proporción 4/3, relación que se establece entre el radio y lado de un octágono. El arquitecto Rafael de la
Hoz Arderius
El radio y lado de un octágono están en
proporción 4/3, como los diseños árabes se basan en cuadrados y octógonos, esta
proporción es una ampliación del cuadrado. La proporción 4/3 se puede localizar en : las bóvedas
cordobesas, las arcadas de la mezquita de Córdoba, el cimborrio de la Catedral de Burgos, las
cúpulas bizantinas,…
Otras aplicaciones prácticas del módulo y la
proporción son las retículas en el diseño editorial.
Un módulo base cuadrado o rectangular se repite y establece
una proporcionalidad con el formato, la caja de texto, y los márgenes.
2.5.
Le Modulor de Le Corbusier.
Una de las preocupaciones de Le
Corbusier fue la modulación. Le Modulor,
de 1949, fue creado para ser un sistema de medidas, para la normalización e
industrialización.
Se construyó con base a la medida humana, tomando como base la progresión de Fibonacci y de la sección áurea. Se parte de un ser humano-modulo de1,83
metros (6
pies ) donde esta presente la sección áurea 1,83 = 0,70 +
1,13, de donde se deducen otras proporciones áureas: 0,... 0,27, 0,43, 0,70,
1,13, 1,83, ... ∞ A esta progresión la
llamó la serie roja.
Se construyó con base a la medida humana, tomando como base la progresión de Fibonacci y de la sección áurea. Se parte de un ser humano-modulo de
Si el ser humano levanta el brazo
hasta la altura de 2,26 m .
tenemos el doble de 1,13 m . O la construcción de
un doble cuadrado. Así se forma otra serie: 0,... 0,32, 0,54, 0,86, 1,40,
2,26,... ∞, a esta nueva progresión le llamó azul. De estas dos series se
obtienen las medidas de el Le Modulor,
que dan una gran posibilidad de
combinaciones al insertar al ser humano en los espacios arquitectónicos, y
ergonómicos.
2.6. Las simetrías.
La
simetría establece una concordancia de unas partes con otras y de las partes
con el todo.
Un
módulo está sometido a movimientos en el plano, si le asociamos fenómenos
físicos como la traslación, la reflexión, el giro, el desplazamiento y la
identidad, se obtienen simetrías.
La
simetría suele tener dos acepciones, una es la de proporción y equilibrio; otra
la relación entre las parte que integran un todo. Una módulo contenido en un
plano puede cambiar de posición por diferentes movimientos. La primera posición
del módulo se le llama la posición inicial u original, una vez aplicado el
movimiento se le transforma en la imagen o posición final. Si tenemos en cuenta
un módulo algunas de las posibilidades de simetrías aplicando movimientos en el
plano serían las siguientes:
1. Traslación.
La
simetría por translación, desplaza el módulo en una dirección y a una distancia
limitada. El módulo queda repetido con la misma orientación. La dirección de
desplazamiento es la dirección de traslación.
2. Reflexión.
La
simetría por reflexión o simetría axial, el módulo rota 180º con respecto a un
eje de simetría. El módulo se separa del plano y vuelve a él mediante una
semirotación, alrededor de la recta fija de giro. El módulo queda invertido y
desplazado a la misma distancia con respecto al eje. Es la simetría propia de
la hoja de los libros, y se encuentra en la mayoría de seres vivos.
3. Giro.
La
simetría por Giro, el módulo contenido en un plano rota a partir de un punto
fijo determinado, llamado centro de giro, y el ángulo de giro que limita la
rotación puede ser dextrógiro o levógiro
La
simetría radial es cuando la rotación puede ser incompleta, por ejemplo un
ángulo de 72º, que al repetirse 360 º produce una simetría radial. Por ejemplo
la simetría de la estrella de mar.
La
simetría central: es cuando hay una rotación con un ángulo de giro llano,
entonces recibe le nombre de simetría central.
4. Desplazamiento.
(Translación
+ Reflexión)
La
simetría por desplazamiento, el módulo tiene al mismo tiempo un movimiento de
traslación y de reflexión.
Se
produce un desplazamiento con simetría, de la misma forma que los pies al
caminar.
5. Identidad.
La
simetría por identidad resulta de la superposición sobre sí mismo del módulo al
producirse una rotación total de 360º sobre su propio eje.
2.7. Interacciones formales.
Los módulos al estar unidos tienen una influencia recíproca. En el campo de la composición modular la interacción de dos módulos puede ser por: distanciamiento, toque, superposición, penetración, unión sustracción, intersección y coincidencia. Estas interacciones permiten apreciar aspectos como: cerca y lejos; delante y detrás; encima y debajo.
Los módulos al estar unidos tienen una influencia recíproca. En el campo de la composición modular la interacción de dos módulos puede ser por: distanciamiento, toque, superposición, penetración, unión sustracción, intersección y coincidencia. Estas interacciones permiten apreciar aspectos como: cerca y lejos; delante y detrás; encima y debajo.
Módulos dados :
1. Distanciamiento.
Existe un
distanciamiento entre los módulos en el espacio.
2. Toque. Contacto.
La proximidad
entre los dos módulos es tal que se tocan entre sí.
3. Superposición.
Un módulo se
coloca encima de otro.
4. Penetración.
Se introduce un
módulo en el interior de otro.
5. Unión.
Los módulos se
juntas para ser una unidad.
6. Sustracción.
Los dos módulos
interactúan de tal modo que se quita una diferencia uno del otro.
7. Intersección.
Hay en encuentro
entre los módulos cortándose entre ellos.
8. Coincidencia.
Los módulos se
ajustan uno con otro concurriendo en la misma situación espacial.
2.8. Estructuras
modulares bidimensionales.
1. Coordinación modular bidimensional.
Módulos simples planos.
El modulo plano es la figura elemental
geométrica y orgánica que se repite y da una forma compuesta más mayor. Una red
de mosaicos consta de filas y columnas y
recubre el plano o el espacio, La condición para que el recubrimiento
modular sea óptimo sin dejar huecos es que los ángulos interiores de los
vértices concurran formando una amplitud de 360º. Los únicos polígonos
regulares que son divisores de 360º, son el triángulo equilátero, el cuadrado y
el hexágono regular, a saber:
A. El cuadrado:
360º/4
=90º. El cuadrado tiene cuatro ángulo
de 90 grados, por lo tanto: 90X4=360, cierra el espacio y no deja huecos.
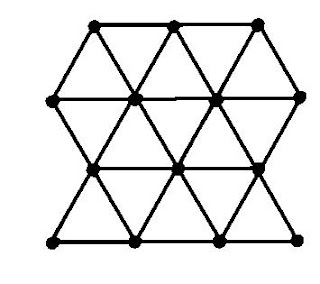
B. El triángulo equilátero:
360º/3
= 120º. El triángulo tiene tres ángulos de120 grados, así: 120X3= 360, compacta
el espacio plano sin dejar fisuras.
C. El hexágono:
360º/6 =
60º. El hexágono tiene seis ángulo de 60 grados, de modo que: 60X6= 60º,
también cierra el espacio.
D. El rombo:
El
rombo es una derivación del hexágono regular y también completa el espacio
plano, 360º/6= 60º y 60X6=360.
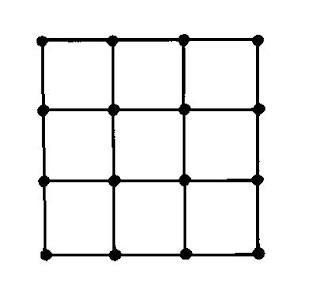
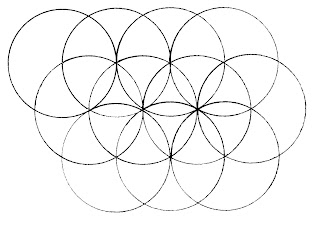
E. La circunferencia:
La
circunferencia es la materia prima (módulo universal) a partir de la cual se
construyen los polígonos que formas mosaicos como el triangulo equilátero,
cuadrado y hexágono. La traslación de la circunferencia una distancia igual a
su radio, forma una red isótropa de círculos que se interseccionan entre sí,
dando lugar a los polígonos base de los mosaicos.
F. El supermódulo.
La combinación de diversos módulos básicos
forma una figura compleja llamada súper módulo.
Otro
aspecto interesante de la modulación en el plano es que aparecen
transformaciones como la traslación y la simetría por reflexión.
2. Coordinación modular bidimensional
Módulos compuestos planos.
Además
de los módulos poligonales de una sola especie, es posible la combinación de
módulos de dos o más polígonos para crear una estructura. Merecen una atención
especial los mosaicos semirregulares, constituidos por más de un polígono
regular y que aparecen en el mismo orden, por ejemplo: el cuadrado y el
triángulo; o el mosaico formado con el hexágono más el cuadrado y el triángulo.
2.9. Estructuras
modulares tridimensionales.
Coordinación modular tridimensional.
Podríamos hacer una diferencia entre la figura, la
forma y la estructura.
A. La forma.
La forma es
tridimensional, 3D. Es el aspecto tridimensional exterior de materia. Las formas al proyectarse sobre los
planos nos dan una imagen, ahora bien las formas pueden tener diversas imágenes
proyectadas dependiendo de su posición, que equivale a diversos aspectos de la
forma o figuras.
Forma de un hexaedro y forma de
un tetraedro
B. La imagen.
La imagen es el efecto
proyectivo de una forma, sobre una superficie, dando lugar a una figura.
Cada imagen es una figura. La
imagen de un tetraedro puede ser un triángulo y la imagen de un hexaedro puede
ser un cuadrado.
C. La figura.
La figura es
bidimensional, 2D. Es un aspecto de la forma.
Puede haber
múltiples figuras para una forma. Por ejemplo en las proyecciones diédricas del
tetraedro y hexaedro: las figuras que puede tener un tetraedro pueden ser un
triángulo equilátero, un cuadrado y un trapecio; y las figuras de un hexaedro
pueden corresponder a un cuadrado, un rectángulo, y un hexágono regular.
D. Estructuras.
La estructura son
las formas organizadas, creadas o construidas con otras formas.
Es la repetición de
un modulo bidimensional o tridimensional.
El módulo plano se
puede componer sobre una red plana y combinarlo formando una estructura
bidimensional. Si trasladamos este proceso a una realidad tridimensional, un
módulo espacial se establece una red
volumétrica.
Una red modular tridimensional utiliza poliedros
que puedan encajar entre ellos sin dejar espacios huecos. Los poliedros que
cumplen estas características son fundamentalmente, el hexaedro, y los prismas.
Un módulo volumétrico puede subdividirse en
submódulos al descomponerlo, o agregarse en supermódulos.
Trabajar en artes visuales con módulos en
relieve, permite una rotación del espectador desde otros puntos de vista y una
modificación del conjunto dependiendo de la iluminación que reciba. Por ejemplo
en la escultura de Alfaro, Oteiza,…
1. Módulos simples tridimensionales.
La
propiedad de rellenar el espacio plano es más sencilla, en cambio para hacer lo
mismo con el espacio sólo el cubo o hexaedro, el poliedro de caras iguales
cuadradas cumple con tal propiedad.
A. El cubo
La
proyección tridimensional del cuadrado es el hexaedro. Como podemos comprobar
el hexaedro tiene ángulos de 90º, y es
divisor de 360º, por consiguiente compacta el espacio.
B. El prisma.
El rectángulo produce prismas
paralelepípedos, que al formar ángulos de 90º , igual que el cubo rellena el
espacio. Ortoedros y hexarromboedros, también pavimentan el
espacio.
Además
de los módulos tridimensionales de una sola especie, es posible la combinación
de módulos tridimensionales de dos o más polígonos para crear una estructura
espacial. Por ejemplo la yuxtaposición del
hexágono más el rectángulo, da el prisma de base hexagonal, varios
prismas se juntan sin dejar espacios libres.
Los
poliedros no regulares que pueden rellenar el espacio por repetición de sí
mismos son:
1.- Cuboctaedro.
2.-
Octaedro truncado, tetracaidecaedro, o poliedro de Lord Kelvin.
3.-
Rombododecaedro, o dodecaedro rómbico.
C. Cuboctaedro.
El Cuboctaedro, es un poliedro de Arquímedes, que se obtiene truncado cada
vértice de un cubo, donde se obtienen caras con forma triangular más el cuadrado.
Los cuboctaedros unidos comprimen el espacio sin dejar espacios vacíos.
Los cuboctaedros, 8 triángulos equiláteros y
6 cuadrados, rellena el espacio.
D. Octaedro truncado, tetracaidecaedro, o poliedro de Lord Kelvin.
El Octaedro
truncado, una variedad del cuboctaedro, se obtiene truncado los vértices de un
octaedro regular. Formado por ocho hexágonos más seis cuadrado, y que procede
del octaedro. Recibe también el nombre de tetracaidecaedro, o poliedro de Lord Kelvin, compacta el espacio por repetición de sí mismo.
El poliedro de Lord Kelvin, 8 caras
hexagonales y 6 cuadrados, compacta el espacio.
E. Rombododecaedro, o dodecaedro rómbico.
El rombo produce uno de los poliedros de Catalan, que también cierra el
espacio sin dejar huecos, llamado
rombododecaedro, o dodecaedro rómbico, formado por doce
rombos iguales. Es otro poliedro que llena el espacio, por clonación de sí
mismo. Su génesis se debe al cubo; si dividimos el cubo en seis diagonales
obtenemos seis pirámides de bases cuadradas y caras triangulares. A cada cara
de un cubo se le pueden pegar esas seis pirámides, el resultado es un
rombododecaedro.
El rombododecaedro, o
dodecaedro rómbico, formado por doce rombos, llena el espacio sin huecos.
2. Módulos compuestos
tridimensionales.
Existen otros módulos tridimensionales que compactan el
espacio pero combinados de dos en dos.
Los poliedros que llena el espacio por combinación en pareja
son la superposición del tetraedro más el octaedro. Los ángulos diedros suman
también 360º.
Otras posibilidades es la combinación de poliedros, si
unimos varios poliedros como:
A. Cuboctaedro y
octaedro
B. Cubo truncado u octaedro.
2.10. El Mosaico.
El mosaico es el recubrimiento
compacto del plano mediante piezas llamadas teselas o baldosas. La composición
puede expandirse hasta el infinito. La historia del arte esta llena de ejemplos
para cubrir suelos, paredes y techos, y
sus derivaciones tapices, bordados, alfombras,… La dinastía nazarita de, Muhammad ibn – Ahmar Ibn Nasr, produjo bellos
alicatados en la Alhambra
de Granada: del àrabe, Al- qata´a, la pieza El estudio de los mosaicos
nazaríes de la Sala
de la Barca de la Alhambra de Granada, es
una fuente de información al módulo, el mosaicos y las simetría de primera
magnitud. Los nombres de las piezas de los mosaicos nazaríes: son estrella o
sino, almendrilla, zafate, candilejo y lazo.
Los mosaicos bizantinos de
Ravena, también son un buen ejemplo didáctico de mosaicos, en especial los
mosaicos de San Vital, San’t Apollinaire in Clase y San’ t Apollinare Novo.
1. Mosaicos formados por una sola tesela y que sea un polígono regular.
La clave para formar un mosaico
es que la suma de los ángulos de cada vértice sea una circunferencia de 360º.
Los divisores de 360º , que forma
el círculo son 3, 4, y 6. De esta forma sólo hay tres polígonos regulares que
compactan el espacio: el cuadrado, el triángulo equilátero y el hexágono
regular.
2. Mosaicos formados por dos
tesela y que sean polígonos regulares.
Además de las posibilidades
anteriores se pueden crear mosaicos formados por más de un polígono regular o
también llamados los semirregulares. Hay ocho mosaicos semirregulares:
E. Triángulo y hexágono.
F. Octógono y
cuadrado.
G. Dodecágono y
triángulo
H. Hexágono,
cuadrado y triángulo.
I. Hexágono,
cuadrado y dodecágono
J. Cuadrado y
triángulo
K. Hexágono y
triángulo
L. Cuadrado y
triángulo
3. Polígonos no regulares que rellenan el plano.
Los polígonos no regulares que
también llenan el espacio plano sería cualquier triángulo con su simétrico que
formaría un paralelogramo cubriría el plano. De igual forma ocurre con los
rectángulos y los rombos. Los paralelogramos pavimentan el plano por
traslación. Es el llamado teselado periódico, cuando es posible encontrar un
patrón de repetición a distancias constantes, copiando el paralelogramo,
trasladándolo y pegándolo.
Existen hexágonos y pentágonos
irregulares que si rellenan el espacio, como la conocida teselación del Cairo,
con un pentágono muy particular, un pentágono con forma de casa.
4. Mosaicos por deformaciones de los polígonos.
Los movimientos a los que están
sujetos los mosaicos son: la traslación, el giro y las simetrías.
Si partimos de un polígono
regular como el cuadrado y eliminamos una parte, añadiéndola en el lado
contraria con una traslación, el cuadrado origen sufre una deformación pero
sigue formando un mosaico. Las deformaciones pueden ser más complejas pero la
propiedad de cubrir el espacio plano se mantiene. Los movimientos a los que
puede estar sometido el módulo original pueden ser traslaciones o rotaciones.
Los mosaicos nazaríes que se realizaron en la Alhambra de Granada,
siguen estos patrones.
Alhambra de Granada. El avión nazarí
Alhambra de Granada. Mosaicos del avión
Alhambra de Granada. La pajarita nazarita
Mosaico de la punta de flecha. Alambra de Granada
Las aportaciones al mundo de los
mosaicos del pintor holandés M. C. Escher son destacables, toma como basé los
mosaicos de la Alhambra y deforma la tesela original para transformarla en
animales, objetos o personas. Posteriormente les aplica transformaciones como
la homotecia, la traslación, el giro y la simetría.
En el siglo XX, el matemático
Roger Penrose, rellenó el espacio plano con los mosaicos que se expanden de
forma no periódica hasta infinito, estos
mosaicos llevan su nombre. Los teselados de Penrose se han encontrado en
patrones de átomos de los cuasicristales. A estos teselados se les ha llamado
aperiódicos porque no permiten encontrar un patrón de repetición a distancias
constantes por traslación.
3.
Estructuras modulares artificiales. Aplicaciones en el arte.
Ejemplos de estructures
modulares artificiales
Los módulos tanto bidimensionales o
tridimensionales se han empleado en la arquitectura, el arte, el diseño, la
decoración, la tecnología,… con diferentes funciones, pueden tener un propósito
constructivo y también un fin decorativo. Algunos ejemplos significativos
serían los siguientes.
En el Egipto Antiguo la tumba de Inherka un techo
decorado con espirales y el sagrado buey Apis, antecedente de las
representaciones micénicas y corintias. El pavimento de mosaicos tiene sus antecedentes
en Egipto.
Los órdenes arquitectónicos de Grecia como el
dórico, jónico y corintio son buenos ejemplos de módulos.
El orden dórico tiene una columna con una
altura de 12 a
14 módulos, el módulo era el radio inferior de la columna, y si tomamos el
diámetro será la mitad, o de 6 a
7 veces la altura . Un ejemplo que merece citarse es el Partenón. El orden
jónico tiene una columna con una altura entre 16 y 17 módulos, de la misma
forma el módulo es diámetro de la base. Una obra con este orden es el templo de
la Atenea Victoriosa
o Atenea Niké, en la
Acrópolis de Atenas.
El orden corintio tienen una columna más esbelta que los anteriores, el
fuste tiene una proporción de 19
a 20 módulos, un monumento construido con este orden es
el templete redondo de Lisicrates en Atenas.
El mosaico es una construcción geométrica
para recubrir el plano, sin dejar huecos, con una clase de polígonos o de
diversas clases. Las manifestaciones de mosaicos más sobresalientes son: el
mosaico romano, el bizantino y el musulmán.
El mosaico de la época romana, realizado con
teselas cúbicas, con pasta de vidrio. El arte musulmán nos dejó en la península
ibérica buenos ejemplos de composiciones modulares como los mosaicos nazarítas
de la Alhambra
de Granada, en concreto la Sala
de la Barca ,
son magníficos ejemplos de mosaicos abstractos con módulos imaginativos, donde
se mezcla la geometría, la matemática y la estética. El mundo hispano musulmán
utilizó con profusión el mosaico por
motivos religiosos como en la mezquita de Córdoba, los Alcázares de Sevilla, o
a decoración externa de la Giralda
de Sevilla.
Otra ciudad fundamental en arte del mosaico
es Ravenna, capital del Imperio Romano de Occidente. De su pasado conserva
mosaicos como los del Mausoleo de Galla Placidia, la basílica de San Apolinar
en Classe y San Apolinar Nova. Los mosaicos bizantinos se extendieron a Venecia
como el pavimento de la
Basílica de San Marcos.
El arte mudéjar nos dejó creativas
decoraciones en las fachadas donde el módulo era el ladrillo visto. Estas ideas estéticas de la decoración
mudéjar fueron recogidas por arquitectos como Antoni Gaudí. En la finca Güell
de Barcelona, Gaudí utiliza motivos modulares en la decoración superficial, así
como en la casa Batlló en las escamas del dragón de la cobertura y el
“trencadís” en el Parc Güell.
El mosaico se trasladó a las vidrieras
románicas, góticas o del modernismo utilizando el módulo con en el vidrio de
color.
Las pinturas sobre cerámicas, pueden aplicar
un motivo geométrico modular que se utiliza como patrón para decorar los
recipientes, como la cerámica hispánica de Talavera, Manises,…
Otros arquitectos que han seguido la línea de
un módulo como base en las obras son: Rafael Moneo en el museo de arte de
Mérida y Santiago Calatrava, en la
Ciudad de las Artes y las Ciencias de Valencia. En
arquitectura el módulos sirve como estructura y decoración del edificio, por
ejemplo rascacielos como: el Southeast Financial Center de Miami, Florida. 1983.
Rascacielos, en Korea como el World Trade Center de Seúl, 1988.
El Banco de China en Hong Kong,
1989. En Barcelona el módulo se aplicó en urbanismo
como L’ Eixample, o el Ensanche de la
ciudad proyectado por del arquitecto Ildefons Cerdà, consta de manzanas en
retícula.
Entre la arquitectura y la ingeniería son
conocidas las modulaciones de: la cubierta del British Museum en Londres. El
cristal ha sido para muchos rascacielos un módulo externo visible. La placa
rectangular del cristal se ha utilizado en la escuela de Chicago. Las cúpulas
geodésicas de Richard Bukminster Fuller,
arquitecto norteamericano célebre por su
cúpula de Montreal 1967.
En el hogar cotidiano los módulos están
presentes en: las esponjas para limpiar en las cocinas, las placas solares,
para extraer energía, el juego del Lego, el tablero de ajedrez y damas, los cristales de invernaderos, las persianas,
las rejas y los cerramientos exteriores.
La industria textil, aplica el rapport a las alfombras que son como
vidrieras en tela. Rapoort es una palabra del inglés, que se refiere a
un paralelogramo fundamental del diseño de la industria textil, como el diseño
de moda, telas, visillos y alfombras. El rapport es un dibujo que repetido
encaja con otros dentro de un paralelogramo.
La era digital también nos ha dejado un
mosaico el píxel. Mosaico de píxeles en la fotografía digital.
La tecnología también aplica el módulo en la
mejora óptima de la óptica como en las facetas de un telescopio o un horno solar con diferentes espejos.
El diseño gráfico, es otra de las artes
visuales que utiliza como la decoración en papelería y los papeles pintados, de
módulos. Dentro de las artesanías como la del mimbre, el punto, el bordado, las
alfombras,… se han dado abundantes y excepcionales composiciones realizadas con
módulos.
La decoración es otro campo de estudio como
las rejillas para realizar módulos en mobiliarios; y decoraciones de ventanas,
balcones, cenefas,…
El mobiliario es una variante de
la artesanía que con los muebles modulares, se relaciona directamente con el
módulo. El tatami es un sistema modular
del Japón, basado en las dimensiones humanas: 90 X 180 cm ..
Módulo de un doble cuadrado, que se utilitza en el habitat. Las esteras de tatami, determinan el
módulo para determinar las proporciones y el espacio funcional de les
habitaciones de la casa japonesa.
Resumen
Módulos y redes.
Relación entre la estructura
y la proporción
en la creación de formas
bidimensionales y tridimensionales.
.
1.
Módulos y redes. concepto.
En artes visuales, se entiende
que es una dimensión que se toma como unidad de medida, norma, modelo o patrón
La acepción más conocida es como parte de un todo que se utiliza como unidad en
una construcción, para establecer las dimensiones y proporciones de un
conjunto. Otra acepción en artes visuales es que el módulo es la forma
elemental que se repite múltiples veces y llega a llenar el espacio
bidimensional o tridimensional.
1.2. Concepto de estructura.
Un módulo es la unidad más pequeña que
organiza una estructura. El módulo es el elemento que estructura la
forma.
1.3. El canon.
El “canon” es regla, medida y modelo es
equiparable al módulo en arquitectura, y regula todas las partes de la
obra. El canon de los antiguos egipcios, el módulo era tomado de la anchura de
la mano, el brazo, el puño cerrado, y el codo. El cuerpo humano se representaba
con un módulo de 18 a
21 puños dependiendo de la época. El
canon de los escultores griegos del siglo V a. C., fue el influyente canon de Policleto que se tomaba la cabeza
humana y estaba contenida unas siete veces y media dentro del cuerpo. Posteriormente este módulo se amplio a
ocho cabezas con Lisipo en la estatua Apoxiomeno;
y ocho y media con el artista Leócares en su obra el Apolo del Belvedere.
1. Canon de perfil de los antiguos egipcios.
2. El canon de los escultores griegos del siglo V a. C.
1.4. Concepto de red.
La red
es un conjunto estructurado de módulos y conectados entre sí, con un patrón
característico.
La red
permite superponer, organizar, circular, o componer elementos o formas. Es la
manera más sencilla de dividir el espacio con una regularidad, por ejemplo con
estructuras de polígonos, como un papel milimetrado o isométrico.
1. Redes planas.
Dentro del campo del dibujo es un
buen ejemplo de red, el papel milimetrado y el papel isométrico que proporcionan
una base gráfica para componer dibujos.
2. Redes espaciales.
La proyección tridimensional de
las redes planas se transforman en redes tridimensionales.
1.5. La malla.
En una tipología en malla cada
nodo tiene una conexión con todos los
nodos de la red, además la malla es una red que no deja espacios huecos en su
estructura.
1. Redes y mallas.
Las redes y mallas pueden ser
simples, cuando su estructura consta de un solo polígono y compuestas, cuando
están formadas por dos o más polígonos
1.6. Módulos, mosaicos y redes en la naturaleza.
En la
naturaleza podemos encontrar estructuras modulares naturales Hay múltiples
ejemplos en el mundo orgánico e inorgánico. La naturaleza que es la
mejor constructora utiliza con frecuencia módulos y estructuras modulares. El ejemplo más paradigmático son las
celdas hexagonales de los panales de las abejas. Existen módulos en el mundo
orgánico como los granos
de maíz en la mazorca de maíz; y módulos inorgánicos como las redes de los
minerales.
Estructuras modulares naturales
Mundo orgánico e inorgánico
1. Módulos en el mundo orgánico
2. Módulos en el mundo
inorgánico.
1.7. Estrategias de composición modular.
Cuando se realiza una composición
modular es posible crear mayor interés visual con algunas estrategias como:
1. La tensión.
La tensión se puede agudizar si
el módulo es irregular o curvado.
2. Los submódulos y súper
módulos.
La combinación de diversos módulos básicos o
submódulos forman una figura más compleja llamada súper módulo.
3. Diferente forma,
color, textura.
El color, forma y texturas diversa pueden dar
un interés visual a la composición.
4. Combinaciones.
Los módulos se pueden combinar para añadir
interés y crear ritmo en la composición.
5. Distorsiones.
El módulo se puede distorsionar mediante las
transformaciones geométricas.
6. Ambigüedad
figura – fondo.
Trabajar la ambigüedad de la figura y fondo
da resultados interesantes para jugar con la percepción.
7. Mezcla de
redes.
La combinación de redes de diferentes tipos
proporcionan resultados poco comunes que atraen la atención al espectador.
1.8. Aplicaciones de la teoría modular en
las artes visuales.
Los movimiento artístico como el Op Art, utiliza
submódulos para dar impresión de tridimensionalidad sobre la superficie plana.
Otros artistas que utilizan módulos son: Víctor Vasarely, Maurits Cornelis
Escher y Piet Mondrian
2.
Relaciones entre la estructura y la proporción en la creación de formas
bidimensionales y tridimensionales.
La proporción es la relación que
hay entre las parte y el todo. Al establecer correspondencias y comparaciones
con los módulos la percepción casi de forma intuitiva nos informa de su
armonía..
2.1. La
razón.
La razón es la comparación de dos
cantidades.
La razón entre dos segmentos es
el vínculo que existe entre ellos, como se relacionan por ejemplo 2/1 = 2.
2.2. La proporción.
La proporción es una relación entre razones,
es una combinación o correlación entre dos o más razones, por ejemplo expresado
de modo matemático:
2/1 = 4/2 = 8/4 = 16/8 = 32/16 . Dicho de
otro modo es una conservación de la razón.
A. La igualdad.
B. Semejanza, homotecia y
escala.
C. La
proporción áurea.
Número áureo, o número de oro, es la razón de
proporción Ф = 0,618,… ∞
El número de oro que se ha utilizado en las
composiciones de las obras artísticas.
El rectángulo áureo y el número de oro Φ . Una de las formas más
utilizadas para encontrar la proporción áurea y el número de oro es construirla
a partir del rectángulo áureo.
2.3. Rectángulos
irracionales.
El módulo elemental es el cuadrado donde
la razón entre sus lados es 1/1 = 1.
La diagonal del cuadrado vale √ 2, si abatimos la diagonal sobre la base
del cuadrado y lo ampliamos se obtiene un rectángulo denominado √ 2 = 1,4142135,... ∞, a partir de este se
obtienen una serie de rectángulos irracionales como √ 3, √
4. √ 5,… Un rectángulo irracional es
aquel que tiene como razón un número irracional.
2.4. Proporción cordobesa, el
rectángulo 4/3.
La
proporción cordobesa es propia de un rectángulo donde la razón de sus lados es
1,3. Rectángulo 4/3, relación entre el radio y lado de un octágono.
2.5. Le Modulor de Le Corbusier.
Le Corbusier creó Le Modular, de 1949, fue creado para ser
un sistema de medidas, para la normalización e industrialización. Se construyócon
base a la medida humana, tomando como base la progresión de Fibonacci y de la
sección áurea. Se parte de un ser humano-modulo de 1,83 metros (6 pies ) donde esta presente
la sección áurea 1,83 = 0,70 + 1,13, de donde se deducen otras proporciones
2.6. Las
simetrías.
La
simetría suele tener dos acepciones, una es la de proporción y equilibrio; otra
la relación entre las parte que integran un todo. Una módulo contenido en un
plano puede cambiar de posición por diferentes movimientos, dando lugar a
simetrías que serían las siguientes: traslación, reflexión, giro,
desplazamiento e identidad.
1. Traslación.
2. Reflexión.
3. Giro.
4. Desplazamiento.
5. Identidad.
2.7.
Interacciones formales.
Los módulos al estar unidos tienen una influencia
recíproca. Estas interacciones pueden ser:
1.
Distanciamiento.
2. Toque.
Contacto.
3. Superposición.
4. Penetración.
5. Unión.
6. Sustracción.
7. Intersección.
8. Coincidencia.
2.8. Estructuras modulares bidimensionales.
1. Coordinación modular bidimensional.
Ejemplos de Estructures modulares
artificiales
Los módulos tanto bidimensionales o
tridimensionales se han empleado en la tecnología con diferentes funciones,
pueden tener un propósito constructivo y también un fin decorativo. Algunos
ejemplos significativos serían los siguientes, el Partenón, los mosaicos
romanos, el mosaico bizantino, la
Alhambra de Granada, el arte mudéjar, y la arquitectura modernista de Antonio Gaudí.
Módulos simples planos.
El modulo plano es la figura elemental
geométrica y orgánica que se repite y da una forma compuesta más grande. Los
únicos polígonos regulares que son divisores de 360º, son el triángulo equilátero,
el cuadrado y el hexágono, todos ellos pavimentan el plano.
A. El cuadrado:
B. El triángulo equilátero:
C. El hexágono:
D. El rombo:
E. La circunferencia:
F. El supermódulo.
La combinación de diversos módulos básicos
forma una figura compleja llamada súper módulo.
2. Coordinación modular
bidimensional
Módulos compuestos planos.
Además
de los módulos poligonales de una sola especie, es posible la combinación de
módulos de dos o más polígonos para crear una estructura, como los mosaicos
semirregulares.
2.9. Estructuras modulares tridimensionales.
Coordinación modular
tridimensional
A. La forma.
B.
La imagen.
C. La figura.
D. Estructuras.
1. Módulos simples
tridimensionales.
La
propiedad de rellenar el espacio plano es más sencilla, en cambio es más
difícil para hacer lo mismo con el espacio tridimensional; sólo el cubo, es el
poliedro de caras iguales que cumple con tal propiedad.
A. El cubo
La
versión tridimensional del cuadrado es el cubo, o hexaedro. Rellena el espacio
sin dejar huecos.
B. El prisma.
El rectángulo produce prismas
paralelepípedos, que al formar ángulos de 90º que también pavimentan el espacio.
C. Cuboctaedro.
D. Octaedro truncado, tetracaidecaedro, o poliedro de Lord Kelvin.
E. Rombododecaedro, o
dodecaedro rómbico.
2. Módulos
compuestos tridimensionales.
Otros módulos tridimensionales
que compactan el espacio pero combinados de dos en dos son:
El cuboctaedro más el octaedro,
su superposición llena el espacio, es la superposición del cubo truncado más el octaedro
A. Cuboctaedro
y octaedro
B.
Cubo truncado u octaedro.
2.10. El Mosaico.
El mosaico es el recubrimiento compacto
del plano mediante piezas llamadas teselas o baldosas. La composición puede
expandirse hasta el infinito.
1. Mosaicos formados por una sola tesela y que sea un polígono regular.
La clave para formar un mosaico
es que la suma de los ángulos de cada vértice sea una circunferencia de 360º.
Los divisores de 360º , que forma
el círculo son 3, 4, y 6. De esta forma sólo hay tres polígonos regulares que
compactan el espacio plano: el cuadrado, el triángulo equilátero y el hexágono.
A. El cuadrado.
B. El triángulo equilátero.
C. El hexágono regular.
2. Mosaicos formados por dos teselas y que sean polígonos regulares.
Son mosaicos formados por más de
un polígono regular o semirregulares.
Hay ocho mosaicos semirregulares:
1.- Triángulo y hexágono.
2.- Octógono y cuadrado. 3.- Dodecágono y triángulo. 4.- Hexágono, cuadrado y triángulo. 5.-
Hexágono, cuadrado y dodecágono. 6.- Cuadrado y triángulo 7.- Hexágono y
triángulo. 8.- Cuadrado y triángulo.
Se pueden formar mosaicos con
polígonos no regulares que rellenan el plano; y mosaicos deformando polígonos.
E. Triángulo y hexágono.
F. Octógono y
cuadrado.
G. Dodecágono y
triángulo
H. Hexágono,
cuadrado y triángulo.
I. Hexágono,
cuadrado y dodecágono
J. Cuadrado y
triángulo
K. Hexágono y
triángulo
L. Cuadrado y triángulo
3. Polígonos no regulares que rellenan el plano.
4. Mosaicos por deformaciones de los polígonos.
3. Estructuras
modulares artificiales. Aplicaciones en el arte.
Ejemplos de
estructures modulares artificiales
Bibliografía.
Arnheim,
Rudolf. 1984. Arte y percepción
visual. Alianza Editorial. Colección Alianza Forma. Madrid.
Dondis.
D.A. La sintaxis de la imagen.
Editorial Gustavo Gili.
Fundación
Caixa de Pensións.1988. Fascinat
Simetría. Museo de la
Ciència de Barcelona.. Fundació Caixa de Pensions.
Le
Corbusier. 1979. El modulor.
Editorial Poseidón. Barcelona.
Munari,
Bruno. 1980. El arte como oficio. Nueva Colección Labor. Barcelona.
Munari,
Bruno. 1973. Diseño y comunicación
visual, contribución a una
metodología didáctica. Editorial Gustavo Gili.
Scott,
Robert Gillam. 1974. Fundamentos
del diseño. Editorial Víctor Lerú.
Wolf,
K.L. 1977. Forma y simetría.
Eudeba.
Wong,
Wucius. 1979. Fundamentos del
diseño bi y tridimensional. Editorial Gustavo Gili.
Bibliografía comentada.
Arnheim,
Rudolf. 1984. Arte y percepción
visual. Alianza Editorial. Colección Alianza Forma. Madrid.
Un manual clásico sobre
percepción muy recomendable.
Dondis.
D.A. La sintaxis de la imagen.
Editorial Gustavo Gili.
Libro clásico sobre sintaxis de
la imagen que explica todos los principios de la organización y composición en
artes visuales.
Wong,
Wucius. 1979. Fundamentos del
diseño bi y tridimensional. Editorial Gustavo Gili.
Buen manual que trata de los
principio del diseño con formas planas y abstractas, incorporando el
vocabulario propio de la materia.

































































































































Este comentario ha sido eliminado por el autor.
ResponderEliminarExcelente trabajo, muy útil para los que nos dedicamos al diseño, felicidades.
ResponderEliminar